2장: 금융 데이터의 통계 분석
목표
2장에서는 금융 데이터 분석에서 중요한 통계와 확률 개념을 익힙니다. 데이터를 수치로 요약하는 방법과 금융 데이터의 분포 특성을 이해하고, 수익률 분포, 변동성 등의 특성을 분석하여 데이터의 기본적인 구조를 파악하는 능력을 기릅니다.
2.1 기본 통계 개념 복습
1. 기술 통계 (Descriptive Statistics)
• 평균 (Mean): 데이터의 중심을 나타내며, 수익률 계산 시 자주 사용됨.
• 중앙값 (Median): 데이터의 중간값을 의미하며, 데이터의 왜곡이 있는 경우 평균보다 유용할 수 있음.
• 분산 (Variance)과 표준편차 (Standard Deviation): 데이터의 변동성을 측정하는 지표. 금융 데이터의 변동성 측정에 자주 사용됨.
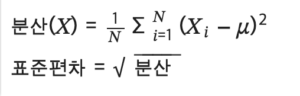
2. 금융 데이터에서의 통계적 요약 지표
• 왜도 (Skewness): 분포의 비대칭성을 나타내며, 금융 데이터가 대칭적인지 여부를 판단할 수 있음.
• 첨도 (Kurtosis): 분포의 꼬리 두께를 나타내며, 금융 데이터에서 극단적 변동성을 측정하는 데 사용.
3. 실습: 기본 통계 지표 계산 및 해석
# AAPL 주가 데이터에서 기본 통계 지표 계산
mean = data["Close"].mean().item() if isinstance(data["Close"].mean(), pd.Series) else data["Close"].mean()
median = data["Close"].median().item() if isinstance(data["Close"].median(), pd.Series) else data["Close"].median()
std_dev = data["Close"].std().item() if isinstance(data["Close"].std(), pd.Series) else data["Close"].std()
skewness = data["Close"].skew().item() if isinstance(data["Close"].skew(), pd.Series) else data["Close"].skew()
kurtosis = data["Close"].kurtosis().item() if isinstance(data["Close"].kurtosis(), pd.Series) else data["Close"].kurtosis()
# 포맷팅을 통해 깔끔하게 출력
print(f"평균: {mean:.2f}")
print(f"중앙값: {median:.2f}")
print(f"표준편차: {std_dev:.2f}")
print(f"왜도: {skewness:.2f}")
print(f"첨도: {kurtosis:.2f}")
3-1. 실습코드 실행결과
평균: 130.31 중앙값: 135.38 표준편차: 30.57 왜도: -0.64 첨도: -0.452.2 금융 데이터의 확률 분포와 특징 분석
1. 확률 분포의 이해
• 정규 분포 (Normal Distribution): 금융 데이터가 정규 분포를 따를 경우 중심 극한 정리에 의해 평균과 표준편차만으로도 데이터의 특징을 설명할 수 있음.
• 포아송 분포 (Poisson Distribution): 드문 이벤트 발생 확률 분석에 사용됨. 예: 거래량의 급증
2. 수익률의 확률 분포 분석
• 로그 수익률 계산: 로그 수익률은 비정상성을 완화하고 데이터의 정상성을 높이는 데 유리함.
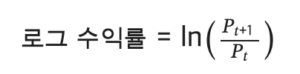
• 변동성 분석: 수익률의 표준편차를 변동성으로 정의하여 금융 데이터의 위험성을 평가할 수 있음.
3. 실습: 수익률 분포 및 변동성 시각화
• 히스토그램과 커널 밀도 추정(KDE)로 수익률 분포 시각화
import numpy as np
data['Log_Return'] = np.log(data['Close'] / data['Close'].shift(1))
# 수익률 분포 시각화
plt.figure(figsize=(10, 6))
sns.histplot(data['Log_Return'].dropna(), kde=True)
plt.title("AAPL 로그 수익률 분포")
plt.xlabel("로그 수익률")
plt.show()3. 실습코드 실행 결과
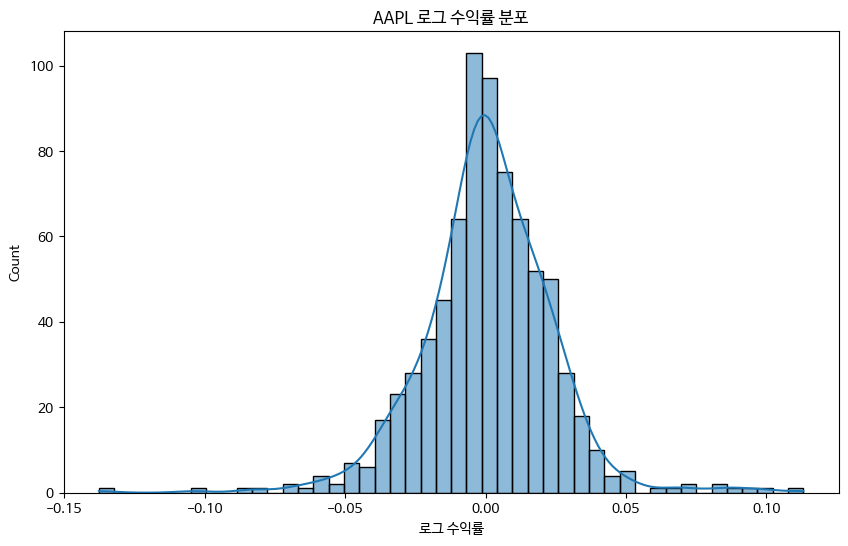
오늘은 금융 데이터 분석에 필요한 기본 통계 지표(평균, 중앙값, 분산, 표준편차)와 금융 데이터의 왜도, 첨도 등 확률 분포 분석을 통해 수익률의 변동성과 분포 특성을 이해하고 시각화하는 방법을 학습했습니다.